
Home > トピックス・イベント > 細胞内シグナル伝達の A-Cellモデル構築ガイド > 基礎
細胞内シグナル伝達のA-Cellモデル構築ガイド 基礎
|はじめに|基礎| 初級| 中級 | 上級| 基礎 解説文PDF|
【基礎】一次反応
概要:細胞内での一次反応の例は多い。たとえば細胞表面のレセプターに結合したリガンドが解離するのは一次反応であるし、Michaelis-Mentenの反応式において酵素基質複合体が分解して生成物が生ずる反応も一次反応である。ここでの説明は一般化して、物質Aが自然に物質Bへと変換される反応(これは放射性同位元素の自然崩壊と同じである)、あるいは複合体LRがそれを構成する物質LとRに分解する反応を例にとる。具体例は「リガンドとレセプターの反応(EGFR)」を参照いただきたい。
ポンチ絵とA-Cellモデル:この簡単な例ではポンチ絵とA-Cellモデルは同じである(図1)。
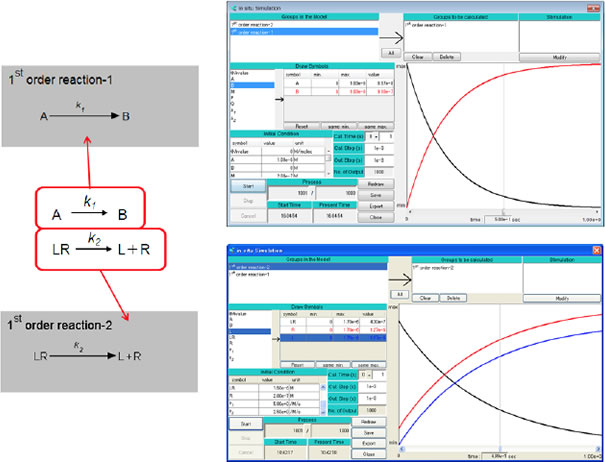
図1一次反応のポンチ絵・A-Cellモデル(左)とシミュレーション結果(右)
ポンチ絵を赤枠内に、A-Cellモデルを灰色四角内に示す。(A-Cellモデルはこちら)。それぞれのシミュレーション結果を右に示す(A-Cellのin situ simulation機能を用いたシミュレーション)。
1st order reaction-1の例では物質AはBに変換されるだけなので、右上に示すシミュレーション結果ではA(黒線)が減少し、B(赤線)が増加する。1st order reaction-2の例では物質LRはLとRに変換されるので、LR(黒線)が減少し、L(赤線)とR(青線)が増加する。2つのグラフが重ならないようにするため、Rの初期値は0ではなく0.2μMに設定したがこれは任意である。この例ではLをリガンド、Rをレセプターと考えれば、レセプター・リガンド複合体LRからの解離反応そのものである。計算条件は計算時間:0~1s、計算時間間隔:1ms、出力時間間隔:1msである。
【基礎】二次反応
概要:二次反応では物質AとBが結合して複合体Cが生成され、タンパク質の複合体形成の基礎的な反応である。たとえば細胞表面のレセプターにリガンドが結合するのは二次反応であるし、Michaelis-Mentenの反応式において基質と酵素が結合して酵素基質複合体が生成する反応も二次反応である。具体例は「リガンドとレセプターの反応(EGFR)」を参照いただきたい。
ポンチ絵とA-Cellモデル:この簡単な例ではポンチ絵とA-Cellモデルは同じである(図1)。
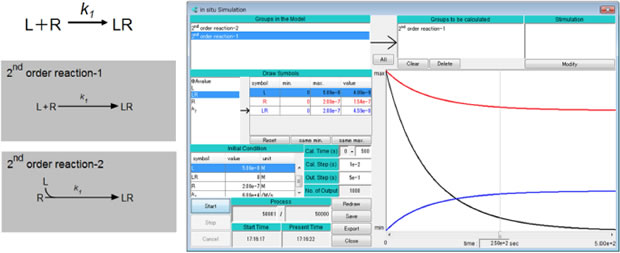
図1二次反応のポンチ絵・A-Cellモデル(左)とシミュレーション結果(右)
ポンチ絵をA-Cellモデルに表したものを灰色四角内に示す。結合反応の表現方法は2種類あり、それぞれの灰色四角内に示す。これは表現法の違いに過ぎないのでどちらでも良く、全く同じシミュレーション結果を与える。下の表現法は、レセプターに2個以上のリガンドが連続的に結合する場合に用いると便利である(「リガンドとレセプターの反応(EGFR)」参照)。シミュレーション結果は図1右のとおりである。A-Cellモデルはこちらとこちら。計算条件は計算時間:0~500s、計算時間間隔:10ms、出力時間間隔:0.5s。
ここでt=0から300秒間、Lが一定濃度で投与され続けた場合のシミュレーションを図2に示す。Lの300秒間投与はA-CellのStimulation機能を使用。A-Cellモデルはこちら。計算条件は同一である。結果は図1とはかなり異なるが、この理由はお考えいただきたい。
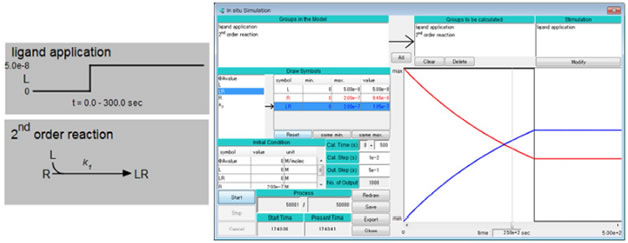
図2リガンドを300秒間投与する二次反応のA-Cellモデル(左)とシミュレーション結果(右)
【基礎】Michaelis-Mentenの反応
概要:酵素反応の代表としてMichaelis-Menten(MM)の反応を取り上げる。MMでは酵素と基質が平衡反応で記述し、生成物が生じるのを一次反応で記述しており、細胞内のシグナル伝達の数理モデルでは多用される。
ポンチ絵とA-Cellモデル:MMも簡単な例であり、ポンチ絵(図1左上)とA-Cellモデル(図1左下の灰色四角内)は同じである。
シミュレーション結果は図1右のとおりである。このパラメータ条件では酵素-基質複合体ES(赤線)が一過性に形成され、生成物P(青線)が時間経過とともに増えてゆく。A-Cellモデルはこちら。計算条件は計算時間:0~50s、計算時間間隔:1ms、出力時間間隔:0.05s。MMでは時間経過に伴って基質が減少して生成物が増加するが、その途中の時間経過はパラメータによって異なったものとなる。A-Cellモデルに含まれる速度定数や初期濃度などのパラメータを様々に変化させ、系の振る舞いがどう変化するか確認していただきたい。
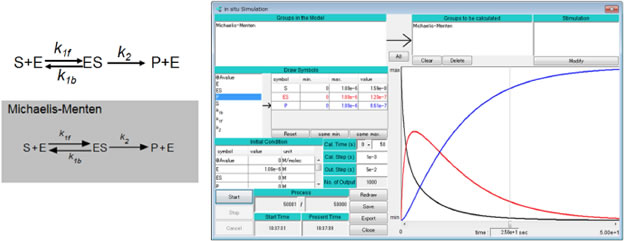
図1Michaekis-Mentenの反応のポンチ絵・A-Cellモデル(左)とシミュレーション結果(右)
【基礎】閉ループ反応
概要:閉ループ反応とは反応出力が次々に伝播して行き、最後の反応出力が入力に戻る一種のフィードバック機構ある.ここでは一次反応で構成した閉ループ反応の例を示す.このような閉ループ反応は,小胞体のカルシウム流出(Calcium Induced Calcium Release: CICR)における正のフィードバック機構や、概日リズムにおける正のフィードバックを含む多重ループの基礎になるものである.
ポンチ絵とA-Cellモデル:図1に示す通りポンチ絵(上)とA-Cellモデル(下)はほぼ同一である.
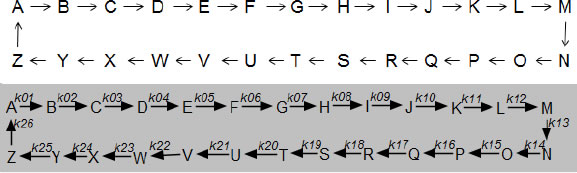
図1 閉ループ反応モデル
A - Zまで26 種類の物質はそれぞれ反応速度定数k01-26にしたがって一次反応で次々に変換される.A-Cellモデルはこちら.ここでは,初期値としてAが1μM,他は0μMで速度定数をすべて同一の0.1 /secとする.計算条件は,計算時間:0~1000 sec,計算間隔:10 msec,出力間隔:1 secとする.
結果は図2の通りである.ループの順番どおりにピークを迎えていることがわかる.この「時間遅れ」が振動のメカニズムになっている.
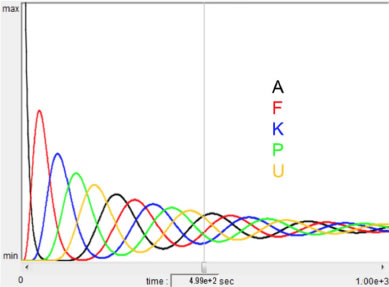
図2 閉ループ反応計算結果
【基礎】単純拡散
概要: 拡散とは、t=0に空間の1点に集中していた物質が時間経過とともに広がり、非常に長い時間の後には物質は空間全体に一様に分布する現象である(図1上)。たとえば細胞内の一か所で合成されたで水溶性タンパク質が広がってゆく現象は拡散で表現される。図1下のグラフは1次元の拡散において時間とともに物質の分布がどのように変化するかを示している。横軸は距離、縦軸は濃度である。t=τでは中心付近の狭い領域に局在しているが、時間の経過とともに領域全体に広がることがわかる。総物質量は保存するので、ピーク濃度(中心の濃度)は低下する。
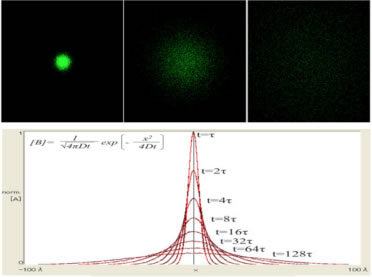
図1拡散の現象
ポンチ絵とA-Cellモデル:拡散をA-Cellでモデル化するのは非常に簡単である。A-Cellの3Dモデル構築ウィンドウで、形態作成→反応式割付→初期濃度・拡散係数設定、の手順を踏めばよい。拡散シミュレーションでは物質が割り付ければよいのだが、A-Cellでは物質のみを割り付けることを許していないので、次のダミーの反応式を作成し、
![]()
拡散させたい領域全体に割り付ける。ポンチ絵を描くことができないくらい単純である(A-Cellモデルはこちら)。kの値は何でも良いが、一応k=0を設定する。拡散定数の設定(ここでは一般的なタンパク質の拡散定数10-11m2/sを設定)とt=0における濃度の設定を行う(ここでは図2左の赤いコンパートメントの濃度を1μMに、それ以外を0とした)。円盤の直径は1μmである。この後はA-Cellからシミュレーションプログラムと初期設定ファイルを生成すればシミュレーションができる。結果を図2右に示す。
シミュレーション結果の見た目は面白くないが、t=0で中心のコンパートメントに局在していた物質が、時間の経過とともに急激に拡散して一様になっていく様子がわかる。
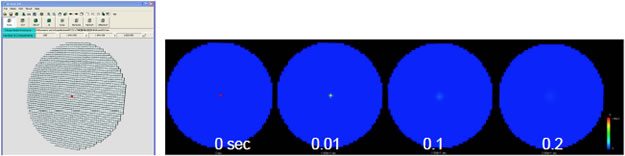
図2単純拡散のA-Cellモデル(左)とシミュレーション結果(右)
文献:米沢富美子、「ブラウン運動」、共立出版、1986, ISBN-10: 4320032365。
Koch, C., “Biophysics of Computation”, Oxford Unv.Press, New York, 2004, ISBN-10: 0195181999.
【基礎】湧き出しがある拡散
概要: 湧き出しがある拡散とは、ある場所から物質が供給され続けてそれが拡散する場合である。たとえば分子量が比較的小さいインポーチンが関与しないタンパク質の核移行や、細胞膜にあるチャネル型受容体が開き、細胞外に高濃度で存在するカルシウムイオンが細胞内へ流入する場合などがこれに相当する(図1)。
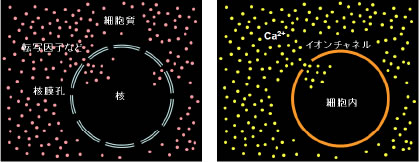
図1湧き出しのある拡散の現象
ポンチ絵とA-Cellモデル:単純拡散の場合と同じようにダミーの反応式を作成して、拡散領域全体に割り付ける。
![]()
やはりポンチ絵を描くことができないくらい単純である。kの値は何でも良い(単純拡散と同じ)。湧き出しをどのようにA-Cellでモデル化するかであるが、Stimulation機能を使う。A-Cellモデルの概要を図2に示す(A-Cellモデルはこちら)。
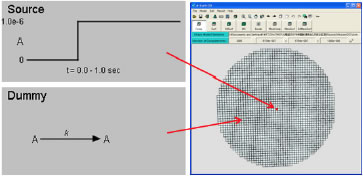
図2 湧き出しのある拡散のA-Cellモデル
このモデルでは直径1μmの円形形態の中心の1つのコンパートメントが湧き出しになっており、t=0から1秒間ここから物質Aが湧き出し続けるという設定になっている。シミュレーション結果を図3に示す。拡散定数は10-11m2/sである。t=0で中心コンパートメントにおけるAの濃度が1μMに固定されるので、
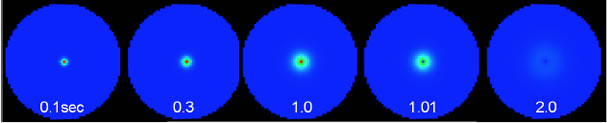
図2湧き出しのある拡散のA-Cellモデル
Aが湧き出し続けることになる。その結果単純拡散のときのようにピーク濃度が低下することなく、Aは全体に広がってゆく。しかしAの湧き出しがt=1秒で終了して以降は0μMに固定されるので今度は中心コンパートメントが吸い込みとなり、濃度が徐々に低下する(t=2秒)。結果を単純の場合と比較してほしい。また湧き出しが複数ある場合や、湧き出しと吸い込みが別の場所に同時に存在する場合なども試してみてはいかがだろうか。











